Difuzija tekočin¶

Fizikalni praktikum 5, Luka Skeledžija, januar 2022¶

Uvod¶

Pri vaji spremljamo pot žarka v nehomogenem plastovitem sredstvu. Lomni zakon se za zvezno spremenljiv lomni količnik posploši na $\cos{\phi} = \frac{\text{konst}}{n(z)}$. Pot žarka skozi kiveto podamo z enačbo:

$\frac{d \phi}{dx} = \frac{dn}{n \cdot dz}$

alt text

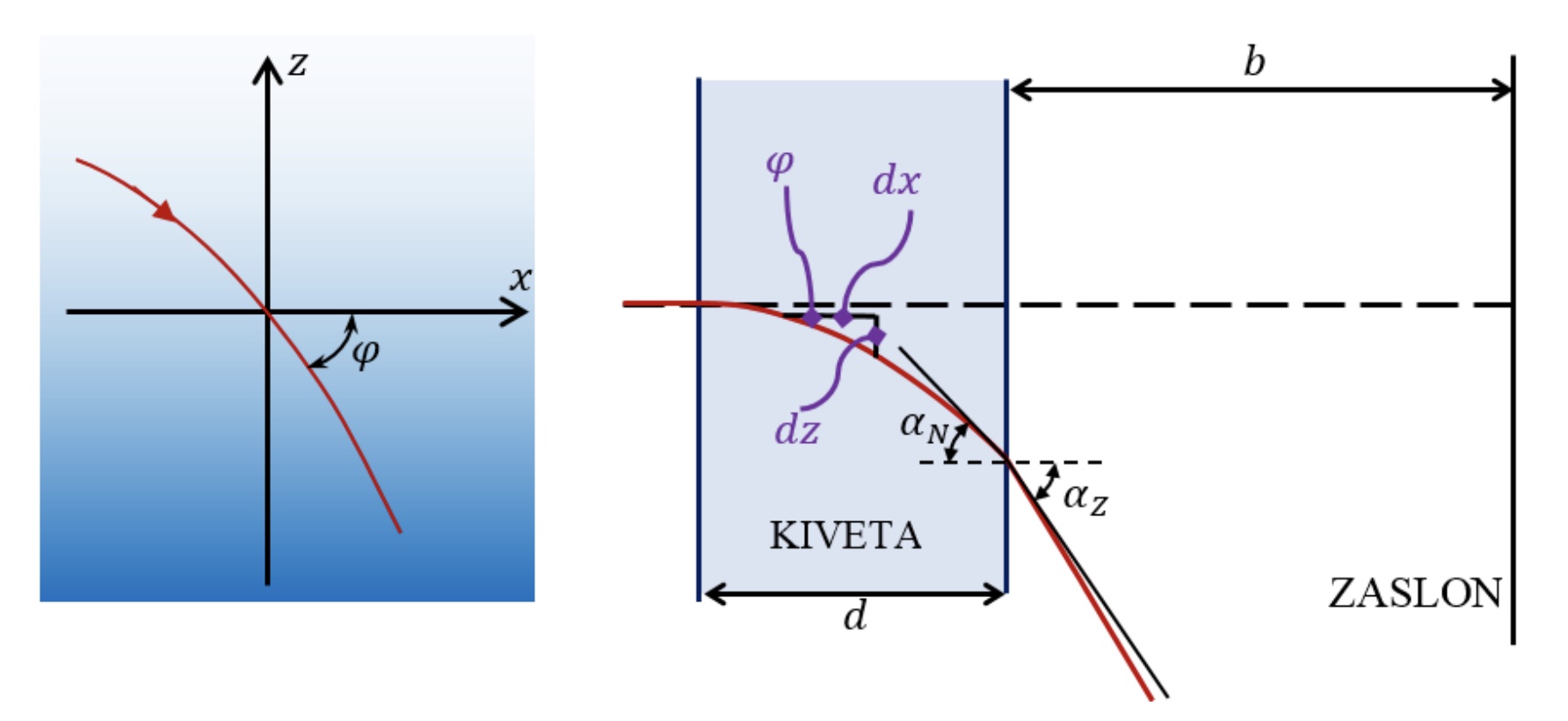
Slika 1: Shematsko prikazana pot žarka

Za majhe kote dobimo odmik $Y = bd \frac{dn}{dz}$. Če obsvetimo kiveto z ravninskim snopom žarkov, nagnjenim za $45^{\circ}$, dobimo na zaslonu krivuljo.

alt text

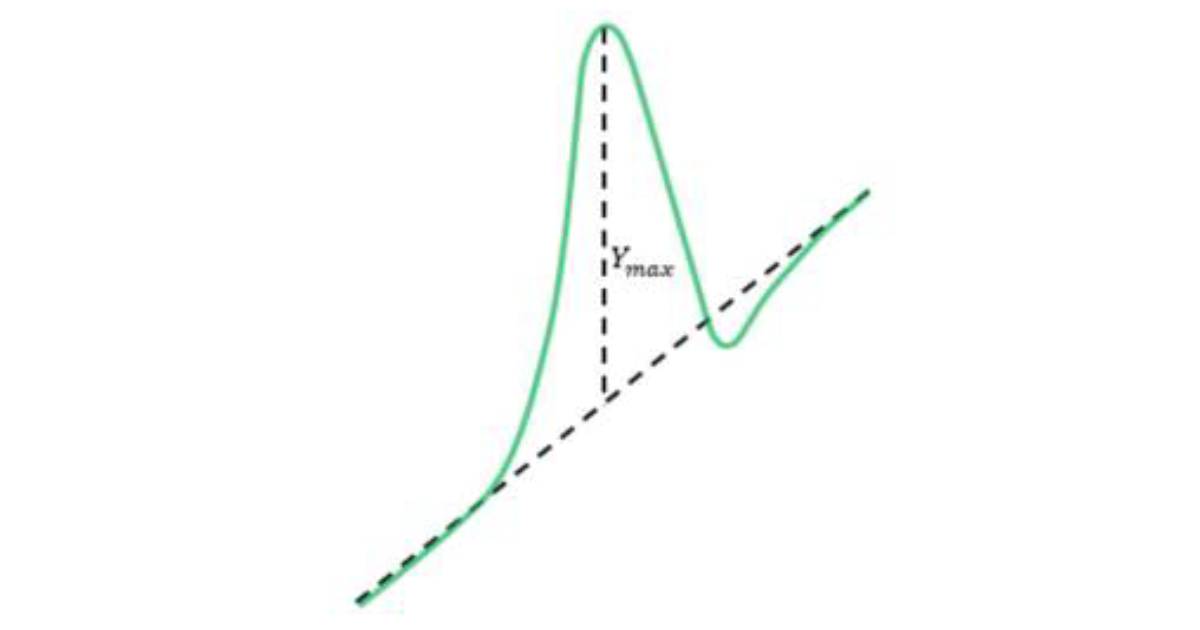
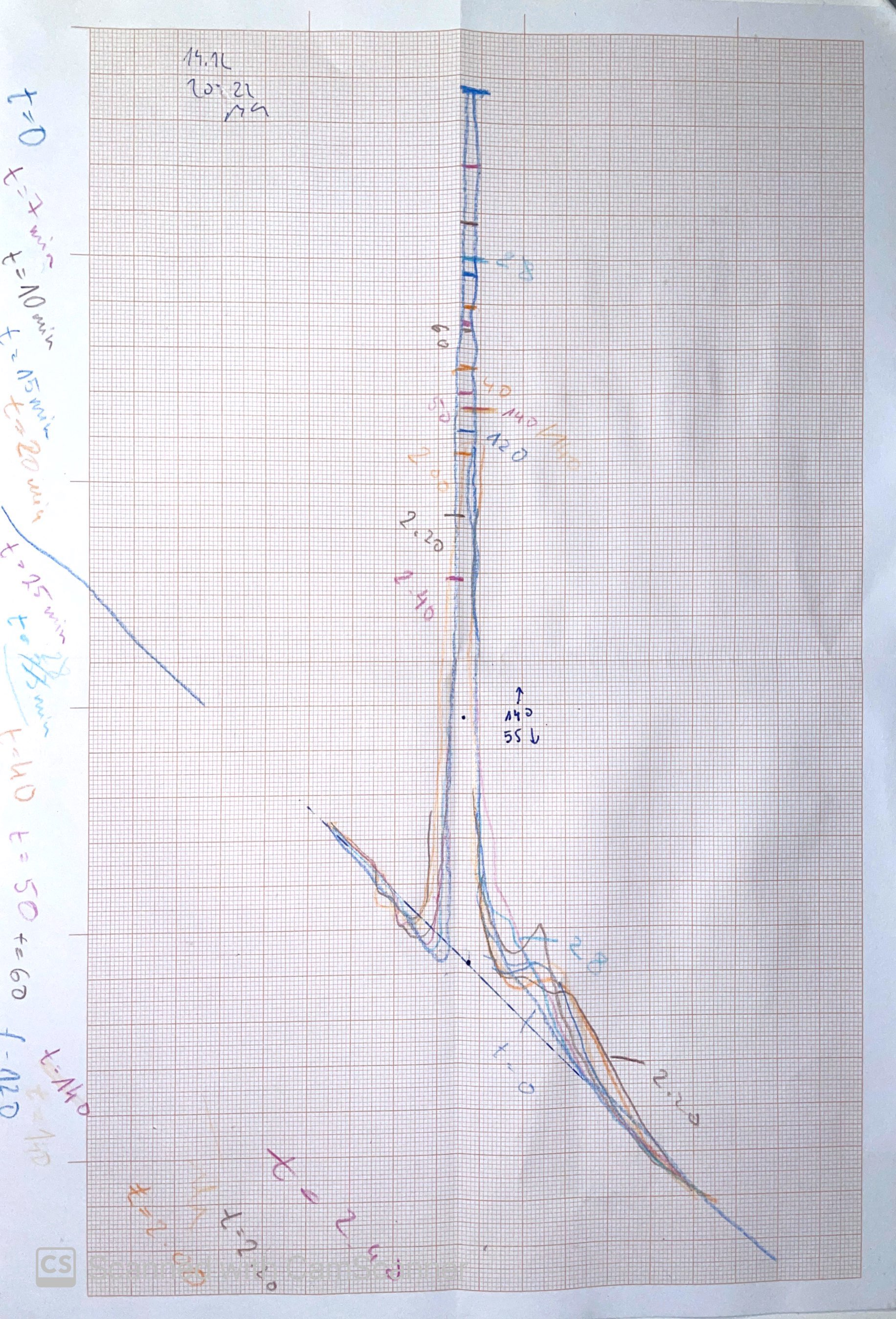
Slika 2: Oblika krivulje kot jo vidimo na zaslonu

Difuzijska enačba za naš primer je:

$ D \frac{\partial^2 f }{\partial z^2} = \frac{\partial f}{\partial t}$

Osnovna rešitev PDE je Greenova funkcija, za naše začetne pogoje pa je rešitev:

$f = \frac{f_0}{2} \left[ 1 + \text{erf} \left( \frac{z}{\sqrt{4 Dt}} \right) \right]$

S predpostavko, da je lomni količnik liearna funkcija koncentracije ga lahko izrazimo kot:

$ n(z) = \frac{n_0 + n_1}{2} + \frac{n_0 - n_1}{2} \text{erf} \left( \frac{z}{\sqrt{4Dt}} \right) $

zato je odmik enak:

$ Y = bd \frac{dn}{dz} = bd \frac{n_0 - n_1}{\sqrt{4 \pi D t}} \exp{\frac{-z^2}{4Dt}}$

Maksimalni odmik pri $z = 0$ je enak:

$ Y_{\text{max}} = bd \frac{n_0 - n_1}{\sqrt{4 \pi D t}} = \frac{S}{k \sqrt{4 \pi D t}}$

kjer je $k$ povečava, $k = (a+b) / a$

Naloga¶

  1. Določiti difuzijsko konstanto D pri stiku etanola in vode

Potrebščine¶

  • laser
  • voda
  • etanol
  • papir
  • kiveta

1. Meritve¶

Z meritvami na milimetrskem papirju smo določili višini krivulje. Izmerili smo tudi sledeče vrednosti razdalj:

  • $a = 21 \pm 1 \, \text{cm}$
  • $b = 79 \pm 1 \, \text{cm}$
  • $d = 11 \pm 1 \, \text{cm}$
  • Podatek $n_0 - n_1 $ prepišemo iz navodil, in sicer $\Delta n = 0.029$
Čas [min] Višina [mm]
0 0 195
1 7 178
2 10 166
3 15 155
4 20 148
5 25 144
6 28 158
7 40 134
8 50 128
9 60 142
10 80 120
11 100 125
12 120 114
13 140 100
14 160 85
Tabela 1: Meritve višine v odvisnosti od časa.

2. Krivulja¶

alt text

Slika 3: Krivulja, ki smo jo izrisovali na papir

3. Rezultati¶

Meritev višine krivulje v odvisnosti od časa nam omogoči določitev difuzijske konstante. Za to potrebujemo še ploščino pod grafom, ki jo lahko izračunamo kot:

$S = \frac{a + b}{a} \, b \, d \, (n_1 - n_0) = (12 \pm 0.5) \cdot 10^{-4} \, \text{m}^2$

Z znano ploščino lahko sedaj narišemo graf odvisnosti $ \frac{1}{4 \pi k^2} \cdot (S / Y_{\text{max}} )^2$ od časa $t$. Ker velja zveza $ D = \frac{1}{t} \cdot \frac{1}{4 \pi k^2} \cdot (S / Y_{\text{max}} )^2$, lahko tedaj difuzijsko konstanto $D$ izrazimo kot naklon premice na omenjenem grafu.

Iz strmine premice lahko tako razberemo vrednost konstante D, dobimo:

$D = 2.6 \cdot 10^{-9} \; \frac{m^2}{s} \; \pm 3.5 \cdot 10^{-10} \; \frac{m^2}{s}$