Osnove mikrovalovne tehnike

Fizikalni praktikum 5, Luka Skeledžija, januar 2023

Uvod

Mikrovalovi so elektromagnetno valovanje z valovno dolžino nekaj cm in frekvenco nekaj GHz. Da ustvarimo mikrovalove, uporabimo klistrone. To so elektronke, ki imajo za pospeševalno mrežico še dve mrežici, ki sta priključeni na pola resonančne votline. Hitrost elektronov se poveča, če kaže polje v isto smer kot njihovo gibanje in obratno. To povzroči hitrostno modulacijo - zgoščine in razredčine v curku. V refleksnem klistronu je na koncu še odbojna elektroda, ki elektrone usmeri nazaj proti katodi. Če je napetost pravilna, curek ojača resonanco v resonančni votlini. Pogoj za povratno zvezo, kjer se lastno nihanje v votlini samo vzdržuje, je izpolnjen pri več diskretnih vrednostih, zato pravimo, da klistron deluje v rodovih.

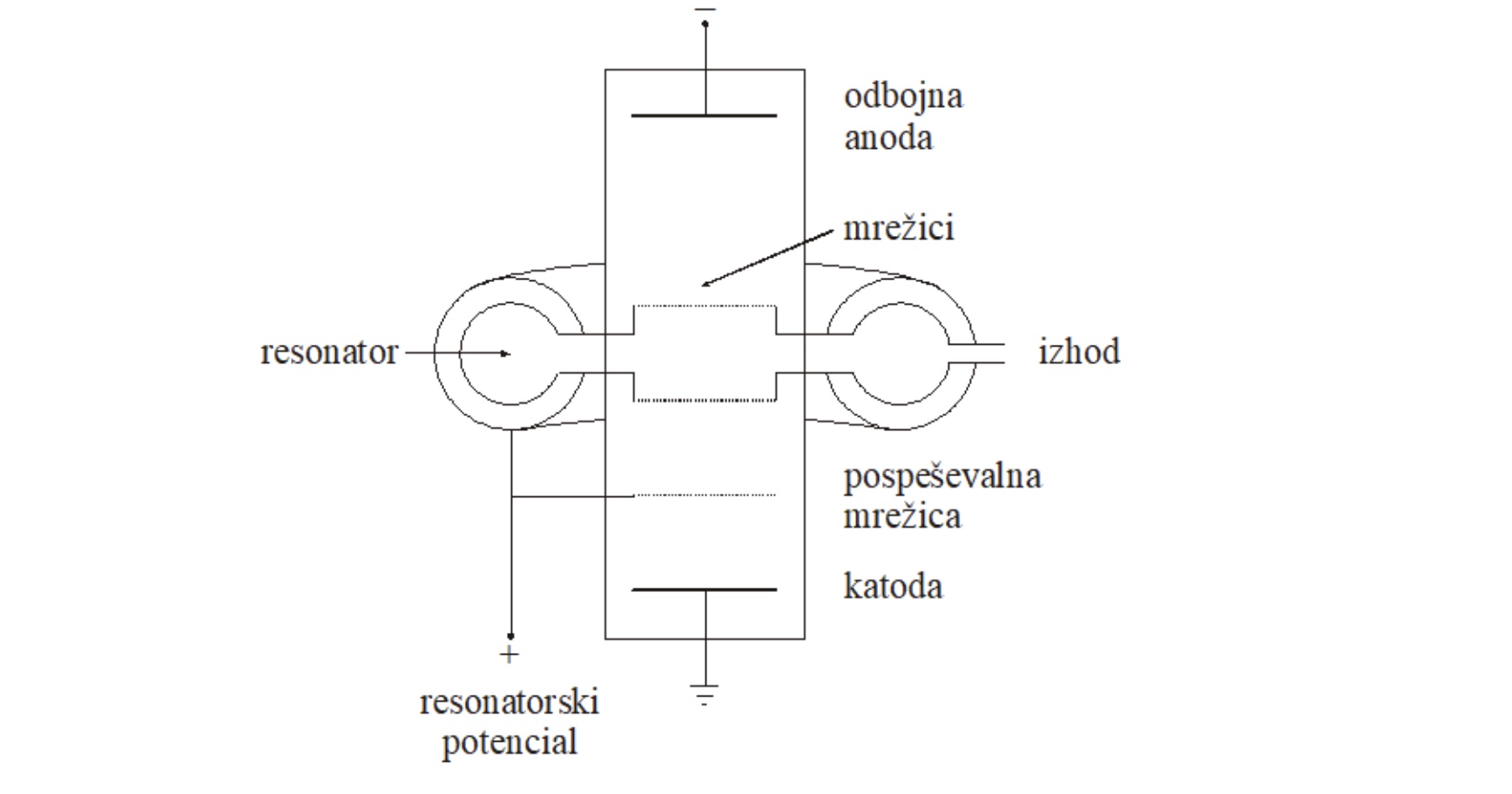
Slika 1: Refleksni klistron

Širjenje mikrovalov

Mikrovalove usmerjamo po valovodih, kjer so upornost, prevodnost, kapacitivnost in induktivnost zvezno porazdeljene (R, G, L, C). Značilna količina za stoječe valovanje v vodniku je razmerje med minimalno in maksimalno amplitudo napetosti - ubranost:

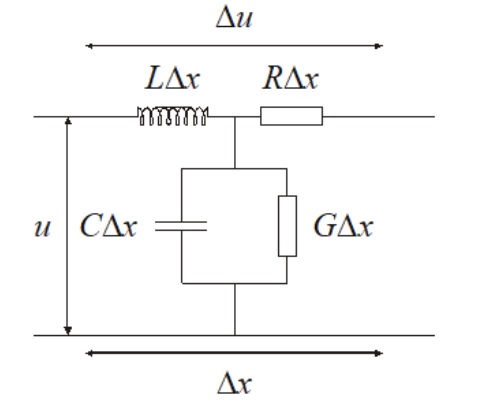
Slika 2: Shematska ponazoritev majhnega dela mikrovalovnega vodnika

Pri vstopu valovanja v valovod se valovna dolžina spremeni in je enaka:

$ s = \frac{|U_{\text{min}}|}{|U_{\text{max}}|} = \frac{1 - |r_B|}{1 + |r_B|} = \frac{|I_{\text{min}}|}{|I_{\text{max}}|} $

Če je vod zaključen z naravnim bremenom in je $Z_R = Z_0$ ni refleksije ($r_R = 0$) in ubranost $s = 1$. Če je vod kratko sklenjen je ubranost $s = 0$ ($ r_R = 1 $). Reaktanca bremena, normirana na karakteristično upornost in enako normirana rezistanca:

$\frac{\eta_R}{Z_0} = \frac{(s^2 - 1) \, \tan{\beta x_{\text{min}}}}{1 + s^2\tan^2{\beta x_{\text{min}}}}$

$\frac{\xi_R}{Z_0} = \left( 1 - \frac{\eta_R}{Z_0} \, \tan{\beta x_{\text{min}}} \right)$

Frekvenca

Frekvenco mikrovalov lahko izmerimo z resonatorjem, ki je vgrajen v valovod. Če je uglašen, se v njem pojavi valovanje, ki pa porabi nekaj moči, zato na osciloskopu vidimo odklon in lahko na ta način preko umeritve izračunamo frekvenco mikrovalov.

Merjenje moči

Moč valovanja merimo s termoelektričnimi elementi, ki se zaradi mikrovalov segrejejo in se jim spremeni upornost - bolometri. Izmerjena moč $P_m$ je z dejansko močjo povezana preko enačbe

$P = \frac{P_m}{1 - |r_R|^2}$

$|r_R|^2 = \left( \frac{1 - s}{1+s} \right)^2$

Spremembo merimo z Wheatstonovim mostičkom.

Določanje impedance iz meritve ubranosti

Ubranost dobimo iz krivulje ubranosti pri priključnem bolometru.

$ s = \sqrt{\frac{h_{\text{min}}}{h_{\text{max}}}} $

Iz krivulje dobimo tudi $x_{\text{min}}'$ in $\lambda '$, ki ju potrebujemo za

$\beta x_{\text{min}} = 2 \pi \frac{x_{\text{min}}'}{\lambda '}$

Naloga

1. Prilagoditi valovod na generator mikrovalov
2. Izmeriti frekvenco valovanja s pomočjo v valovod vgrajenega resonatorja
3. Posneti rodove klistronovega delovanja v odvisnosti od odbojne napetosti
4. Izmeriti moči, ki jih porablja termistor v vrhovih najmočnejših rodov
5. Z osciloskopom posneti krivulji ubranosti za valovod, ki je zaključen z bremenom in za kratko sklenjeni valovod.

Potrebščine

• generator mikrovalov
• osciloskop
• valovod z zaključki
  

1. Rodovi delovanja klistrona

2. Frekvenca valovanja

Frekvenco valovanja izmerimo direktno z mikrometrskim vijakom. Minimum na osciloskipu smo določili pri 4.11 mm.

3. Krivulje ubranosti

V sorazmernosti s časom

CH1 v tem primeru predstavlja lego v odvisnosti od časa.

V sorazmernosti z razdaljo

Primerjava frekvence

Iz grafa 1 razberemo razdaljo med dvema minimumoma $\Delta x = 2.71 \, \text{cm} \pm 0.14 \, \text{cm}$, ki je ravno 1/2 valovne dolžine. Valovno dolžino $\lambda '$ v valovodu pretvorimo v $\lambda$ in dobimo frekvenco:

$\nu = 8.74 \, \text{GHz} \pm 0.42 \, \text{GHz}$,

kar lahko primerjamo s prej izmerjeno frekvenco $\nu \approx 8.44 \, \text{GHz}$.

Ubranost

Upoštevamo enačbo $ s = \sqrt{\frac{h_{\text{min}}}{h_{\text{max}}}} $ in izračunamo

Iz teorije $\rightarrow s_{\text{kratkostična}} = 0 $

$s_{\text{boltometer}} = 0.67 \pm 0.05$

$|r_R|^2 = 0.04 \pm 0.01$

Reaktanca in rezistanca bremena

Določimo še:

$x_{\text{min}}' = 0.98 \, \text{cm} \pm 0.15 \, \text{cm}$

$\beta x_{\text{min}} = 2\pi \frac{x_{\text{min}}'}{\lambda '} = 1.8 \, \text{cm} \pm 0.3 \, \text{cm}$

$\frac{\eta_R}{Z_0} = \frac{(s^2 - 1) \, \tan{\beta x_{\text{min}}}}{1 + s^2\tan^2{\beta x_{\text{min}}}} = 0.26 \pm 0.1$

$\frac{\xi_R}{Z_0} = \left( 1 - \frac{\eta_R}{Z_0} \, \tan{\beta x_{\text{min}}} \right) = 1.41 \pm 0.3$

$ | \frac{Z_R}{Z_0} | = \sqrt{(\frac{\eta_R}{Z_0})^2 + (\frac{\xi_R}{Z_0})^2} = 1.43 \pm 0.9$