Uvod¶
The physics behind Hall's effect in n-type semiconductors¶
Hall's effect refers to the voltage that is generated perpendicular to an electric current flowing through a conductor when it is placed in a magnetic field. This effect is named after physicist Edwin Hall, who first observed it in 1879. In an n-type semiconductor, the current is carried by negatively charged electrons, which are the majority carriers. When a magnetic field is applied to the semiconductor, it exerts a force on the electrons, causing them to move in a direction perpendicular to both the electric current and the magnetic field. This movement of electrons creates an electric field that is perpendicular to both the direction of the current and the direction of the magnetic field, resulting in the production of a voltage. The magnitude of the voltage generated by Hall's effect is directly proportional to the strength of the magnetic field and the amount of current flowing through the semiconductor. It is also proportional to the mobility of the electrons in the semiconductor, which is a measure of how easily they can move through the material. This means that the Hall voltage is higher in semiconductors with high electron mobility, such as some types of silicon. Hall's effect is used in a variety of applications, including the measurement of magnetic fields and the determination of the carrier type and concentration in semiconductors. It is also used in the production of magnetic field sensors, which are found in a wide range of devices, from smartphones to cars.
*Generated with ChatGPT by OpenAI*
1.1 Hallova napetost¶
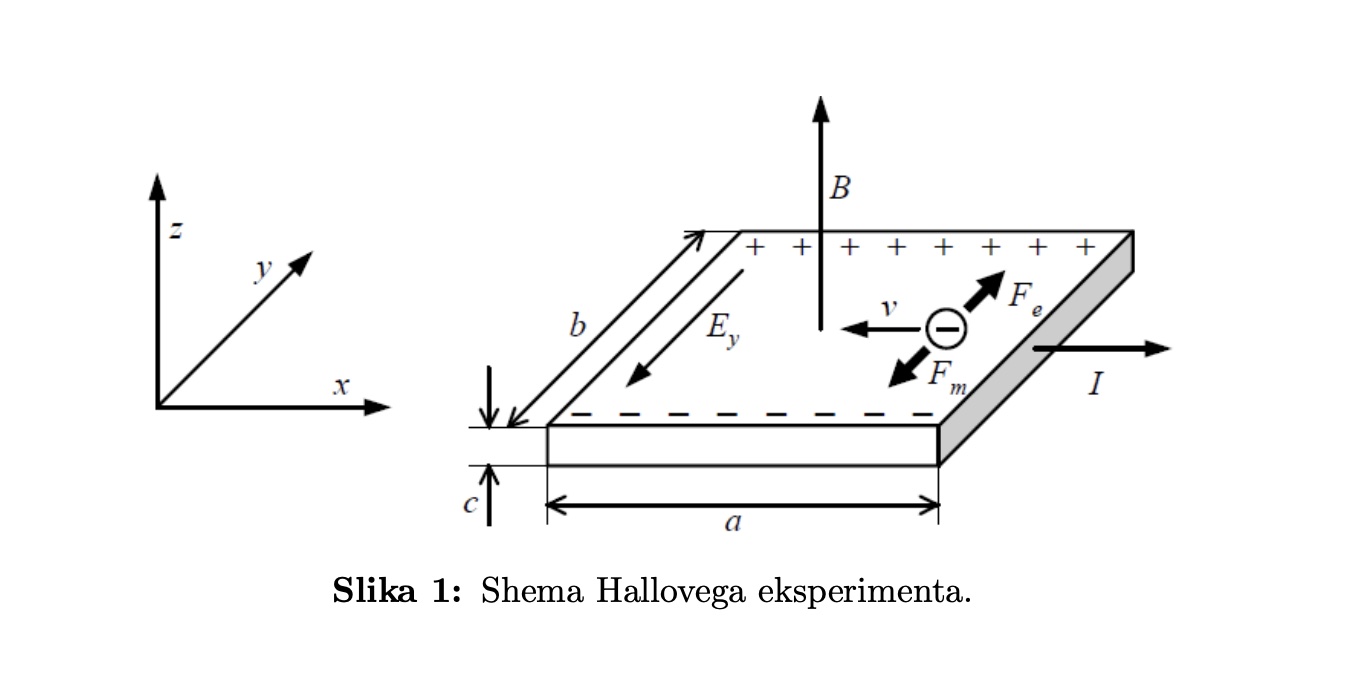
Pravokotno izrezan kovinski trak s stranicami $ a $, $b$ in $c$ po katerem teče električni tok $I$ v smeri osi $x$, postavimo v prečno magnetno polje $B$ v smeri osi $z$. Predpostavimo, da so nosilci naboja elektroni z nabojem $−e_0$. Gostota toka $j = I/(bc)$ je za elektrone podana tudi z izrazom $ j = − ne_0v $, kjer sta $n$ in $v$ gostota ter hitrost naboja. Elektroni zaradi magnetne sile $ F_m = e_0vB$, ki deluje v smeri osi $-y$, začnejo kopičiti ob robu kovinskega traku. Tam se nabere plast negativnega naboja, na drugi strani, kjer je primanjkljaj elektronov, pa plast pozitivnega naboja. Ti dve plasti ustrvarita prečno električno polje $E_y$ v smeri osi $-y$ in s tem električno silo $F_e = e_0(−E_y) = e_0E_y$, ki ravno uravnovesi magnetno silo. V stacionarnem stanju velja $F_m + F_e = 0$, torej
$e_0E_y = e_0v_B$.
Iz tega sledi izraz za velikost prečnega električnega polja $E_y$:
$E_y = vB = − jB ne_0$.
Hallova napetost $U_H$, ki nastane zaradi prerazporeditve naboja med robovoma kovinskega traku, je definirana kot:
$U_H = E_yb = − jBb ne_0 = − IB ne_0c$.
Kvocient $E_y/jB$ imenujemo Hallova konstanta in ga označimo z $R_H$:
$R_H = − ne_0 = U_Hc IB$
Hallov pojav lahko uporabumo za merjenje gostote magnetnega polja B.
1.2 Hallov pojav v polprevodniku tipa n¶
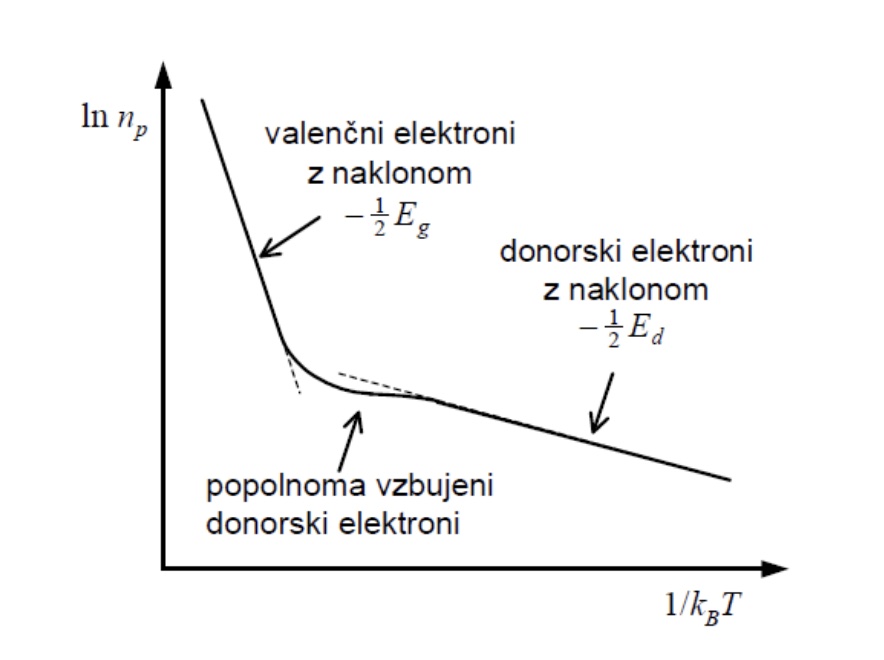
Gostota nosilcev naboja se v polprevodniku drastično poveča ob prisotnosti primesi, ki se vgradijo v polprevodniški kristal. Kristal čistega polprevodnika običajno sestavljajo štirivalentni atomi kot sta germanij in silicij. Če dodamo primes petvalentnih atomov (npr. arzen) se ta vgradi v strukturo štirivalentnih atomov in ima tako en odvečni elektron. Ta elektron potrebuje zelo majhno energijo, da se od njega odtrga in skoči v prevodni pas. Dodatni donorski nivo tako leži tik pod prevodnim pasom. Energijsko režo označimo z $E_d$. H gostoti elektronov v prevodnem pasu (polprevodnika tipa n) prispevajo tudi elektroni, ki so bili termično dvignjeni iz donorskega nivoja. Iz velekanonične porazdelitve dobimo naslednji izraz v limiti nizkih temperatur:
$n_p(T) = N_d^{\frac{1}{2}} \left( \frac{m_e k_b T}{2 \pi h^2} \right)^{\frac{3}{4}} \exp{\left( -\frac{E_d}{2k_b T} \right)}$,
kjer je $N_d$ gostota donorskih primesi. Ko pa je terminčna energija dovolj velika, so v prevodni pas vzbuheni vsi donorski elektroni:
$n_p(T) = N_d$
Iz zgornjega je razvidno, da lahko z merjenjem Hallove napetosti izmerimo temperaturno odvisnosti gostote nosilcev naboja v polprevodniku tipa n in preverimo ustreznosti zgoraj zapisanih izrazov.