Sunkovna jedrska magnetna resonanca

Fizikalni praktikum 5, Luka Skeledžija, januar 2023

Uvod

Jedro v homogenem magnetnem polju

Jedro ima poleg vrtilne količline $\vec{\Gamma}$ tudi magnetni moment $\vec{\mu}$. Sprememba njegove vrtilne količine je sorazmerna sunku navora:

$\frac{d\vec{\Gamma}}{dt} = \vec{M} = \gamma \vec{\Gamma} \times \vec{B_0}$

iz česar sledi, da vrtilna količina (magnetni moment) precedira okrog smeri Magnetnega polja z Larmorjevo krožno frekvenco $\omega_L = \gamma B_0$. Kadar magnetizacija ni vzporedna s smerjo magnetnega polja $B_0$, precesira okrog njegove smeri z Larmorjevo frekvenco. V ravnovesnem stanju pa je magnetizacija $\vec{M}$, ki je posledica orientacije magnetnih momentov atomskih jeder v vzorcu, obrnjena vzdolž smeri megnetnega polja $\vec{B_0}$ zaradi povečanja posameznih momentov.

Vpliv kratkotrajne visokofrekvenčne motnje na magnetizacijo v statičnem magnetnem polju

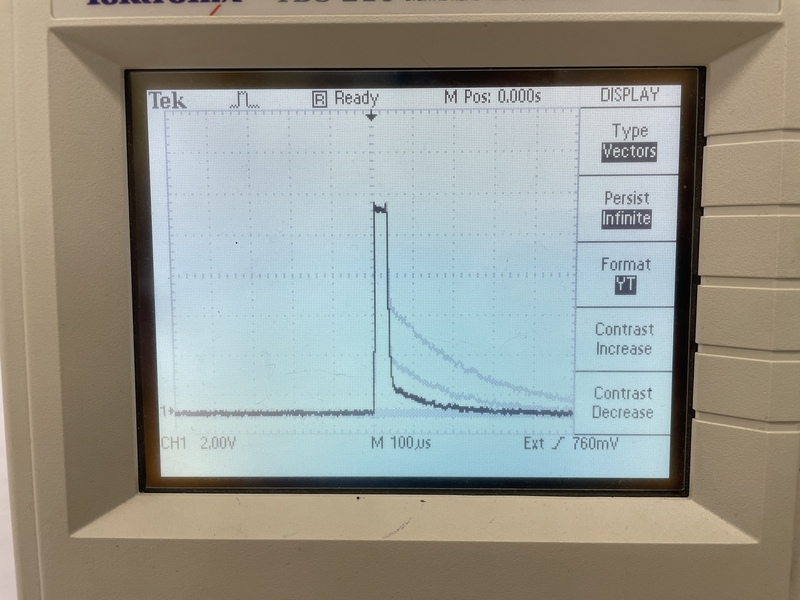
Ko za kratek čas $T$ vključimo magnetno polje $B_1$, ki oscilira z Larmorjevo frekvenco $ω_L = \gamma B_0$ in kaže v smeri osi $x$ (pravokotno na smer statičnega magnetnega polja), se kot $\theta$ med magnetizacijo in statičnim magnetnim poljem $B_0$ poveča. Sunek $\pi / 2$ obrne magnetizacijo, ki v ravnovesnem stanju kaže vzdolž osi z $x’$, v smer $y’$. Na precesijo posameznega magnetnega momenta vplivajo poleg zunanjih magnetnih polj tudi naključno se spreminjajoča polja magnetnih momentov drugih jeder in elektronov. Smer, v katero kaže posamezen magnetni moment, se zato s časom statistično odmika od prvotne smeri in se vrača v termodinamsko ravnovesno vrednost. Projekcija magnetizacije $\vec{M}$ na ravnino $x’y’$ zato eksponentno pada z razpadno konstanto $T_2$, ki jo imenujemo transverzalni oziroma spinsko-spinski relaksacijski čas. Energija magnetnih momentov jeder v magnetnem polju se ne spreminja. Poleg izgube fazne povezave se zmanjšuje tudi azimut posameznega magnetnega momenta $\theta_i$. Projekcija magnetizacije na os $z’$ se zato povečuje s karakterističnim časom $T_1$, ki ga imenujemo longitudinalni oz. spinsko-mrežni relaksacijski čas.

$M_z = M(1 − \exp \frac{-t}{T_1}) $

Vidimo, da se v tem primeru celotna energija magnetnih momentov jeder v statičnem magnetnem polju spremeni, torej je posredi interakcija magnetnih momentov jeder z magnetnimi momenti elektronov v atomih, kar termodinamsko pomeni ohlajanje sistema.

Spinski sistem v nehomogenem magnetnem polju

Posamezen magnetni moment čuti poleg notranjih magnetnih polj še razliko med poljem na mestu magnetnega momenta in povprečnim magnetnim poljem. Razlika povzroči precesijo posazmenih magnetnih momentov v vrtečem se sistemu okoli osi $z’$ z različnimi frekvencami v različnih smereh. Projekcija magnetizacije v ravnino $x’y_0$, v nehomogenem magnetnem polju ne pada več eksponentno s karakterističnim časom $T_2$, ampak kot neka druga krivulja, katere oblika je odvisna od $T_2$, nehomogenosti magnetnega polja in oblike vzorca. Navadno karakteristični čas padanja te krivulje označimo s $T^*_2$. Približek nehomogenosti magnetnega polja je tedaj:

$\Delta B_z = \frac{1}{T^*_2 \gamma}$

NMR spektrometer

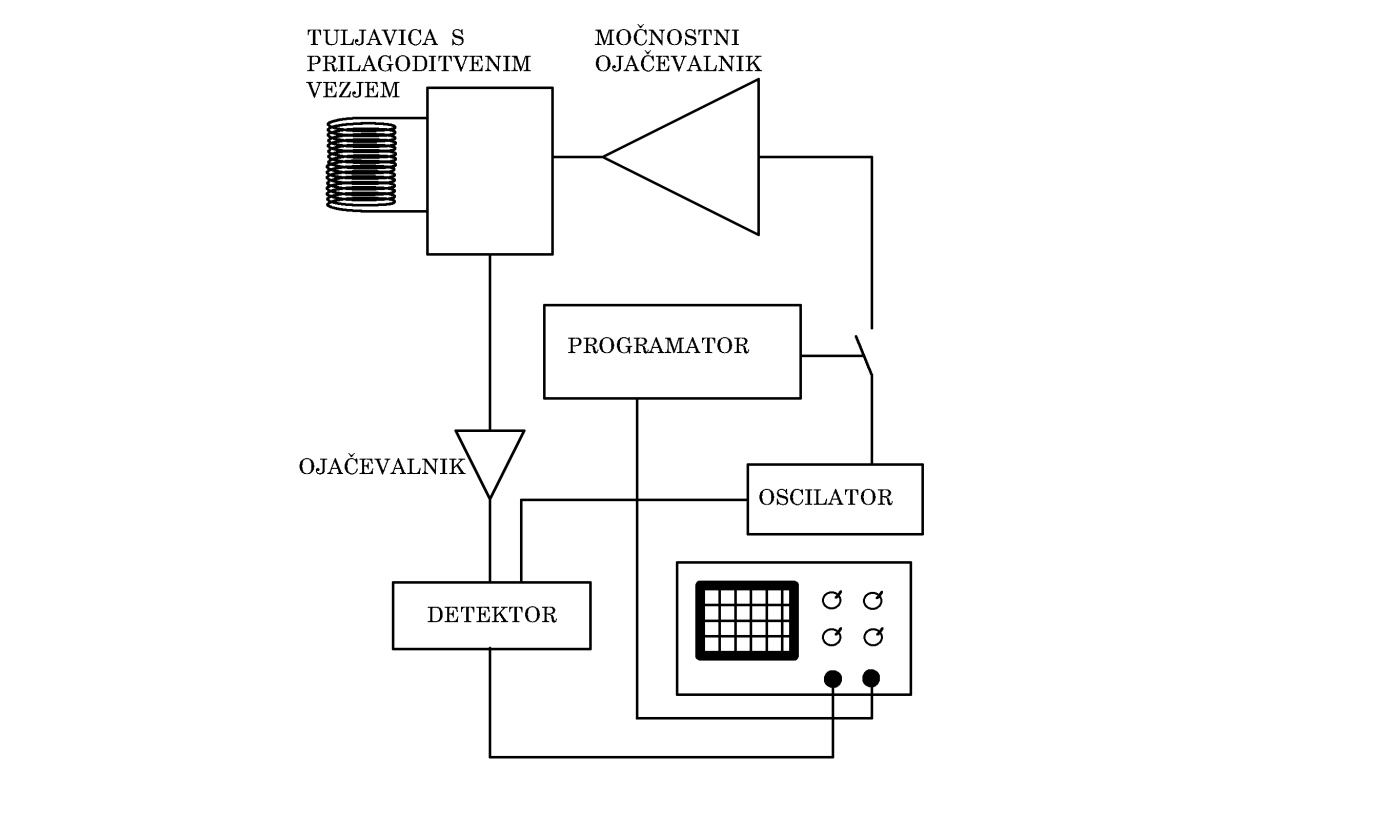
Slika 1: Shema NMR spektrometra

Naloga

1. Za vzorec vode s primešanimi paramagnetnimi ioni posikati signal proste precesije po sunku $\pi /2$ in signal spinskega odmeva po zaporedju sunkov $\pi /2$ in $\pi$. Z opazovanjem širine signala procste precesije in signala spinskega odmeva poiskati takšno lego sonde, da bo magnetno polje v področju vzorca čimbolj homogeno. Iz obeh širin izračunati $T^*_2$ in oceniti nehomogenost magnetnega polja v vzorcu.
2. Z opazovanjem odvisnosti signala proste precesije med dvema sunkoma $\pi /2$ določiti relaksacijski čas $T_1$, za vzorec vode s primešanimi paramagnetnimi ioni in za vzorec vodovodne vode.
3. Za vodo s primešanimi paramagnetnimi ioni posikati odvisnost višine signala spinskega odmeva od presledka $\tau$ med sunkoma $\pi /2$ in $\pi$ in določiti spinsko-spinski relaksacijski čas, $T_2$

Potrebščine

• NMR spektrometer
• osciloskop
• vzorci vode
  

1. Izračun $T^*_2$ in nehomogenost magnetnega polja

Vzorec vode s primesjo ionov najprej postavimo v magnetno polje. Nastavimo trajanje sunka $\pi / 2$ tako, da maksimiziramo amplitudo signala proste precesije. Na osnovi dolžine eksponentnega pojemanja tako izmerimo čas $T^*_2$. Sliko z osciloskopa uvozimo v WebPlotDigitizer, ročno poklikamo točke na krivulji in uvozimo .csv v Python. Dobimo spodnjo krivuljo.

$T^*_2 = 22 \mu \text{s} \pm 5 \mu \text{s}$

Zdaj lahko uporabimo spodnjo enačbo in ocenimo še $\Delta B_z$, kjer je $\gamma = 2.675$:

$$\Delta B_z = \frac{1}{T^*_2 \gamma} = 0.017 \, s^{-1} \pm 0.004 \, s^{-1}$$

Umeritev skale za časovne zamike med sunki

Za meritve zakasnitve med sunkoma je najprej potrebno umeriti skalo gumba.

2. Amplituda signala proste precesije v 2. sunku v odvisnosti od zakasnitve med sunkoma

Na podlagi meritve in fita določimo prek enačbe $U = U_0 (1 - \exp{\frac{-t}{T_1}})$ vrednost $T_1$ za vodo s paramagnetnimi ioni:

$T_1 = 2.29 \, \text{ms} \pm 0.01 \, \text{ms}$

Enako meritev ponovimo še z vodovodno vodo, le da je v tem primeru to precej težje. Dolžino sunkov podaljšamo 100x. S funkcijo PERSIST na osciloskopu izrišemo spodnjo sliko in iz nje izračunamo iskano vrednost $T_1$ za vodovodno vodo.

Vodovodna voda

Slika 3: Intenziteta drugega sunka pri spreminjajočem se zamiku

Na primeru vodovodne vode dobimo pričakovano veliko večji $T_1$ in ogromno napako fita, saj poizkušamo prilagoditi celotno funckijo na samo 3 točke. Smo pa približno zadeli velikostni razred.

$T_1 = 0.1 \, \text{s} \pm 0.1 \, \text{s}$

3. Spinski odmev

V zadnjem delu smo izmerili še odvisnost amplitude spinskega odmeva od dolžine zakasnitve med sunkoma. V tem primeru se lahko ravnamo po enačbi:

$U = U_0 \exp{\frac{-2t}{T_2}}$

Iz parametrov fita smo dobili vrednost $T_2$ za vodo s primesmi:

$T_2 = 2.39 \, \text{ms} \pm 0.01 \, \text{ms}$