Elektronska spinska resonanca

Fizikalni praktikum 5, Luka Skeledžija, januar 2023

Uvod

Elektron je delec s spinom $S = \frac{1}{2}$ in ima magnetni moment, katerega velikost je:

$ \mu_B = \frac{eh}{2m_e} = 9.27 \cdot 10^{-24} \; \text{J/T} $

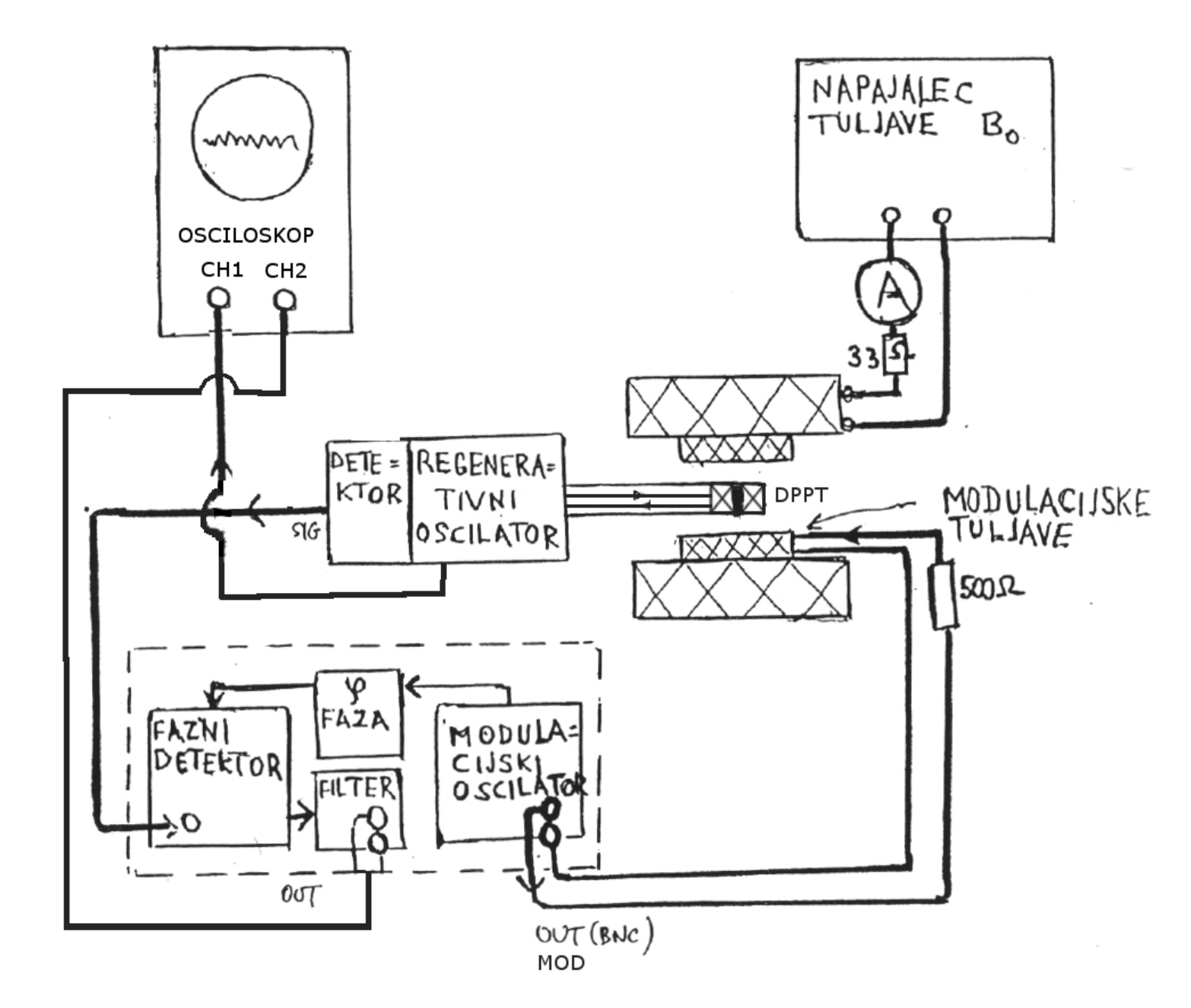
V zunanjem magnetnem polju $B_0$ sta možni dve orientaciji, med njima je energijska razlika $ \Delta E = g \mu_b B_0 $. Prehode lahko vzbujamo z elektromagnetnim sevanjem, kjer mora veljati $ \Delta E = h \nu $. Iz tega lahko izrazimo razmerje med frekvenco in gostoto zunanjega polja, za prost elektron je to razmerje enako $ \nu / B_0 = 28.026 \; \text{GHz} / \text{T} $. Ker je relativna populacija obeh nivojev podana z Boltzmannovo porazdelitvijo, se občutljivost veča z večanjem frekvence in z njo magnetnega polja. Zaradi interakcij elektrona s kristalno mrežo, z drugimi elektroni ali jedri, resonančne črte niso ostre, ampak razširjene ali razcpeljene. Vzorec se nahaja v tuljavi resonančnega kroga regenerativnega oscilatorja. Ko doseže zunanje magnetno polje $B_0$, vrednost, ki izpolnjuje resonančni pogoj, nastopi absorpcija visokofrekvenčnega valovanja in amplituda oscilacij oscilatorja pade. Obučajno je amplituda modulacije manjša od širine absorpcijske črte in v tem primeru dobimo signal modulacijske frekvence, katerega amplituda je proporcionalna odvodu absorbcijske črte v odvisnosti od statične komponente polja. Da izboljšamo razmerje signala proti šumu uporabimo fazni detektor.

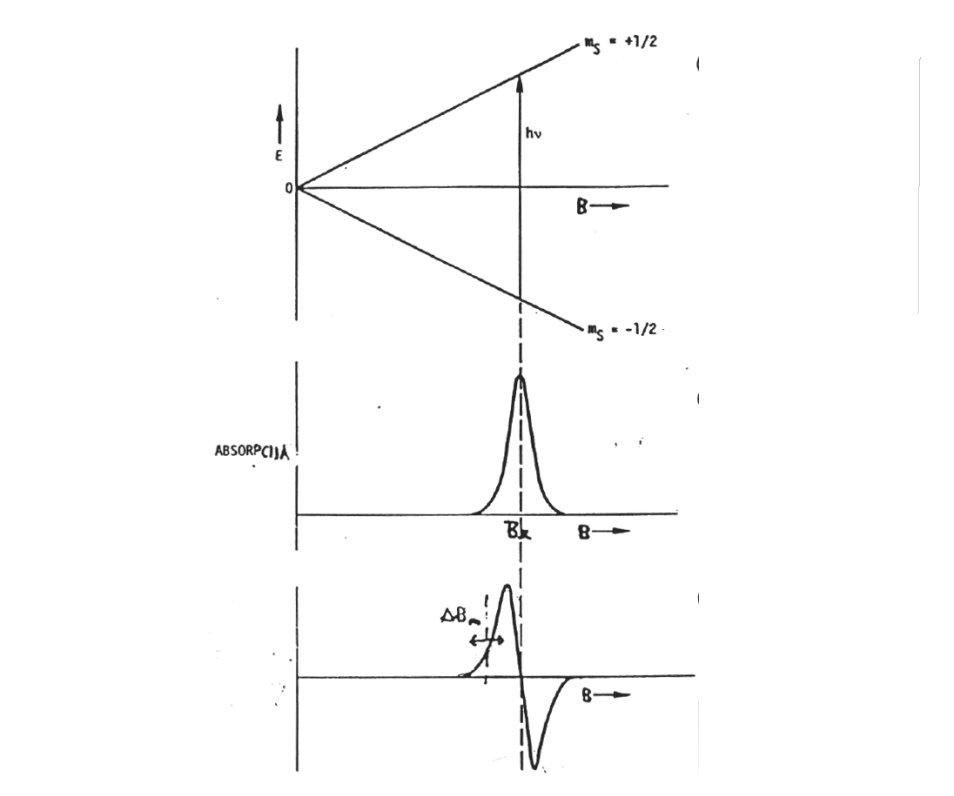
Slika 1: Diagram energijskih nivojev elektronav magnetnem polju (zgoraj) in absorpcija energije v odvinsosti od magnetnega polja (sredina) ter amplituda ESR signala na izhodu detektorja (spodaj)

Naloga

1. Z vzorcem DPPH kot merjencem določiti g-faktor prostega elektrona in razmerje $B / \nu$
2. Izmeriti širino absorpcijske črte

Potrebščine

• osciloskop
• napajalnik
• modulacijske tuljave
• regenerativni oscilator
• modulacijski oscilator
• fazni detektor

Slika 2: Shema eksperimenta

1. Meritve

V uvodu smo navedli, da je razmerje med responančno frekvenco $\nu$ in gostoto magnetega polja $B_0$ konstantno in za prosti elektron enako $28.086 \, \text{GHz}$. Podobno, želimo za naš eksperiment določiti razmerje $ \nu / B_0 $ in s pomočjo spreminjanja toka $I$ izmeriti odvod resonančne krivulje po jakosti zunanjega magnetnega polja $B_0$. S pomočjo odvoda lahko tako izračunamo širimo resonančne krivulje $\Delta B$. S pomočjo razmerja $\nu / B_0$ pa lahko določimo giromagnetno razmerje $g$ za elektron.

Slika 3: Diagonala v tuljavi - diagonalo izračunamo po pitagorovem izreku kot $d = \sqrt{l^2 + (2R - h)^2}$, kjer je $h = 2 \cdot d_{\text{žice}} \cdot N_l / N$

Količina	Vrednost
Št. ovojev $N =$	$1557$
Št. ovojev po dolžini $N_l =$	$72 \pm 2$
$N_l / N =$	$21.625 \pm 1$
$d =$	$18.3 \, \text{cm} \pm 0.2 \, \text{cm}$
$\frac{B_0}{I} = \frac{\mu_0 \cdot N}{d} = $	$10.7 \, \text{mT/A} \pm 0.2 \, \text{mT/A}$

V nadaljevanju poizkusimo iz merjenih podatkov določiti vrh resonančne krivulje. Odčitamo tok, kjer je vrednost odvoda resonančne krivulje enaka (oz. najbližje) 0. Tako določenemu toku $I_0$ izračunamo pripadajoči $B_0$ ter dobimo:

2. Odvod absorpcijske črte po $B$

S faznim detektorjem smo izmerili odvod absorpcijske črte tako, da smo spreminjali tok $I$ (posledično $B$) v majhnih korakih in z osciloskopom odčitavali izhod iz faznega detektorja. Širina absorpcijske črte $\Delta B$ je definirana kot razmik med ekstremoma odvoda. Enako meritev smo izvedli pri treh različnih frekvencah (tj. 80, 85 in 90 MHz).

$\nu$ [MHz]	$I_0$ [mA]	$B_0 (I_0)$ [mT]	$\Delta B$ [mT]	$ \frac{\nu}{B_0} $ [GHz/T]	g
80.45 ± .08	277.00 ± 2	2.96 ± .03	0.13 ± 0.1	27.17 ± 2.1	1.94 ± 0.2
85.00 ± .08	294.00 ± 2	3.14 ± .03	0.12 ± 0.1	27.06 ± 2.1	1.93 ± 0.2
90.09 ± .08	316.00 ± 2	3.38 ± .03	0.14 ± 0.1	26.66 ± 2.1	1.90 ± 0.2

Tabela 1: Določene količine za frekvence 80, 85 in 90 MHz.

3. Spreminjanje resonančne frekvence pri konstantnem B

V drugem delu vaje opravimo še eno meritev, pri kateri ohranjamo konstanten $B$ ($I_0 = 295 \pm 2$ mA) in spreminjamo frekvenco. Ker velja, da je razmerje $\nu / B$ konstantno, ima to početje podoben efekt kot meritev prej. Če smo prej peljali tangento po absorpcijskem vrhu s spreminjanjem $B$, tokrat premikamo sam absorpcijski vrh skozi fiksen $B$.

$I_0$ [mA]	$\nu_0$ [MHz]	$B_0 (I_0)$ [mT]	$\Delta B$ [mT]	$ \frac{\nu}{B_0} $ [GHz/T]	g
295 ± 2	85 ± 0.1	3.16 ± .03	0.14 ± 0.1	26.93 ± 2.1	1.92 ± 0.2

Tabela 2: Določene količine za $I_0 = 295$ mA.