Uvod¶
Izvor žarkov X¶
Elektrone ki izhajajo iz katode pospešimo z visoko napetostjo proti kovinski tarči. Pri trku zaradi zaviranja elektronov v polju jeder nastanejo X žarki - zavorno sevanje. Če imajo elektroni zadosti energije, pa lahko iz notranjih elektronskih lupin izbijejo izbijejo elektrone. Elektroni iz višjih stanj zapolnijo vrzel, pri tem pa izsevajo karakteristične X žarke z določeno energijo. V refleksnem klistronu je za mrežicama resonančne votline odbojna elektroda, ki neenakomerni elektronski curek usmeri nazaj proti meržicama in katodi. Moduliran curek se med mrežici vrne s tako fazo da ojači lastno nihanje elektromagnetnega polja v resonančni votlini in klistron deluje kot oscilator.
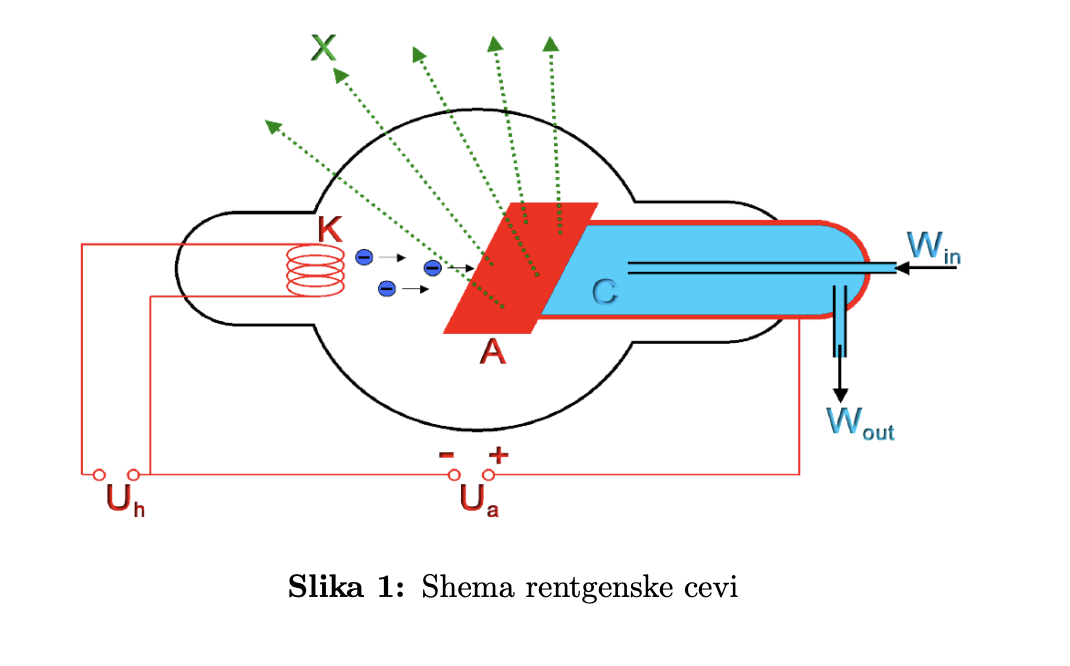
Slika 1: Shema rentgenske cevi
Ionizacijska celica¶
Najenostavnejša ionizacijska celica je kar ploščni kondenaztor zvezan z izvoromo visoke napetosti. Če v prostor med ploščama posvetimo z rengenskimi žarki, ti na atomih zraka povzročijo fotoefekt. Fotoelektroni zaradi svoje kinetične energije ionizirajo molekule. Nastale ionske pare napetost na kondenzatorju usmeri k ploščam in tako dobimo na tokokrogu tokovni sunek. Če jih je veliko, se sunki povprečijo v merljiv električni tok. Pojem števila fotonov pa se pri rentgenskih napravah redko uporablja, namesto tega se govori o hitrosti ekspozicijske doze (As/kgh) ali absorbirane doze (Gr/h).
Ekspozicijska doza X je električni naboj $ \Delta Q$, ki ga v zraku volumna $ \Delta V $ z maso $ \Delta m $ na enoto mase sprosti ionizirajoče sevanje:
$ \frac{dx}{dm} = \frac{\Delta I}{\Delta m} $,
kjer $\Delta I$ pomeni tok nabitih delcev. Omenjeni tok nasičenja v ionizacijski celici je torej merilo za hitrost ekspozicijske doze.
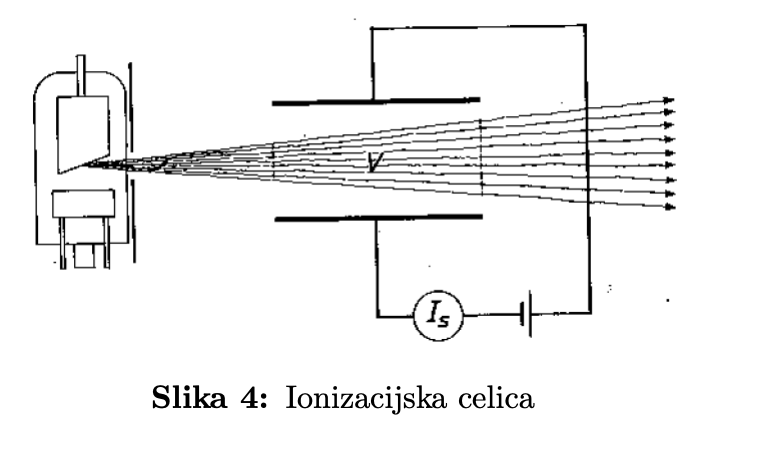
Slika 2: Ionizacijska celica
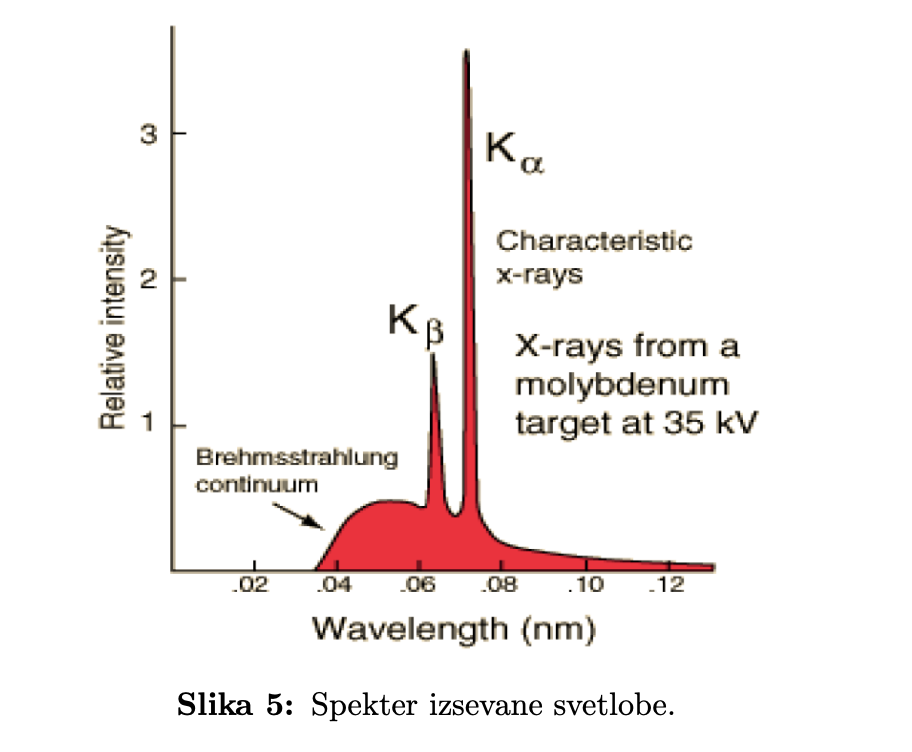
Slika 3: Spekter izsevane svetlobe
Polariziranost žarkov X¶
Žarki X nastanejo v rengentski cevi zaradi interakcije pospešenih elektronov z jedri v anodi. Frekvenca izsevanega elektromagnetnega valovanja ν je določena s kinetično energijo $ \Delta E_k $, ki jo izgubi elektron:
$ \Delta E_k = h \nu $,
kjer je $ h $ Planckova konstanta. Maksimalno frekvenco dobimo takrat, ko se vsa elektronova kinetična energija pretvori v elektromagnetno. Naboj niha v smeri osi Y, s pospeškom $a_z$. Po pospeševanju naboja sledi sevanje elektromagnetnega valovanja, ki ga opišemo z vektorjem jakosti električnega polja $ \vec{E} $ in vektrojem magnetne poljske gostote $ \vec{B} $. Ker naboj niha v smeri osi $ Y $, ima $ \vec{E} $ vedno isto smer. Pravimo, da je tako polje linearno polarizirano.
Koherentno sipanje žarkov X¶
Pri interakciji žarkov X z elektroni se energija fotonov ne spremeni. Nas zanima predvsem elastično sipanje, ker z njim določamo polarizacijo žarkov X. Z merjenjem tega sipanja lahko določimo polariziranost rentgenske svetlobe. V snop postavimo sipalec, nato pa v ravnini XZ z nekim števcem za ionizirajoče sevanje izmerimo kotno porazdelitev sipanega valovanja. Dobljena porazdelitev je krog, če valovanje ni polarizirano in elipsa če je polarizacija delna. V praksi merimo le vrednosti $ I_x $ in $ I_z $, polariziranost pa definiramo z izrazom:
$ \eta = \frac{I_z - I_x}{I_z + I_x} $