Holografija

Fizikalni praktikum 5, Luka Skeledžija, oktober 2022

Uvod

Holografija je posebna vrsta fotografije, ki omogoča tridimenzionalno ponazoritev predmeta. Pri navadni fotografiji zabeležimo na fotografski film ali ploščo projekcijo porazdelitve gostote svetlobnega toka, ki ga seva predmet. Projekcijo dosežemo s pomočjo optične leče. Slika je dvodimenzionalna, ker ob gledanju slike manjšega predmeta pred večjim ne moremo videti zastrte dele, četudi bi usmerili pogled na fotografijo pod različnimi koti.

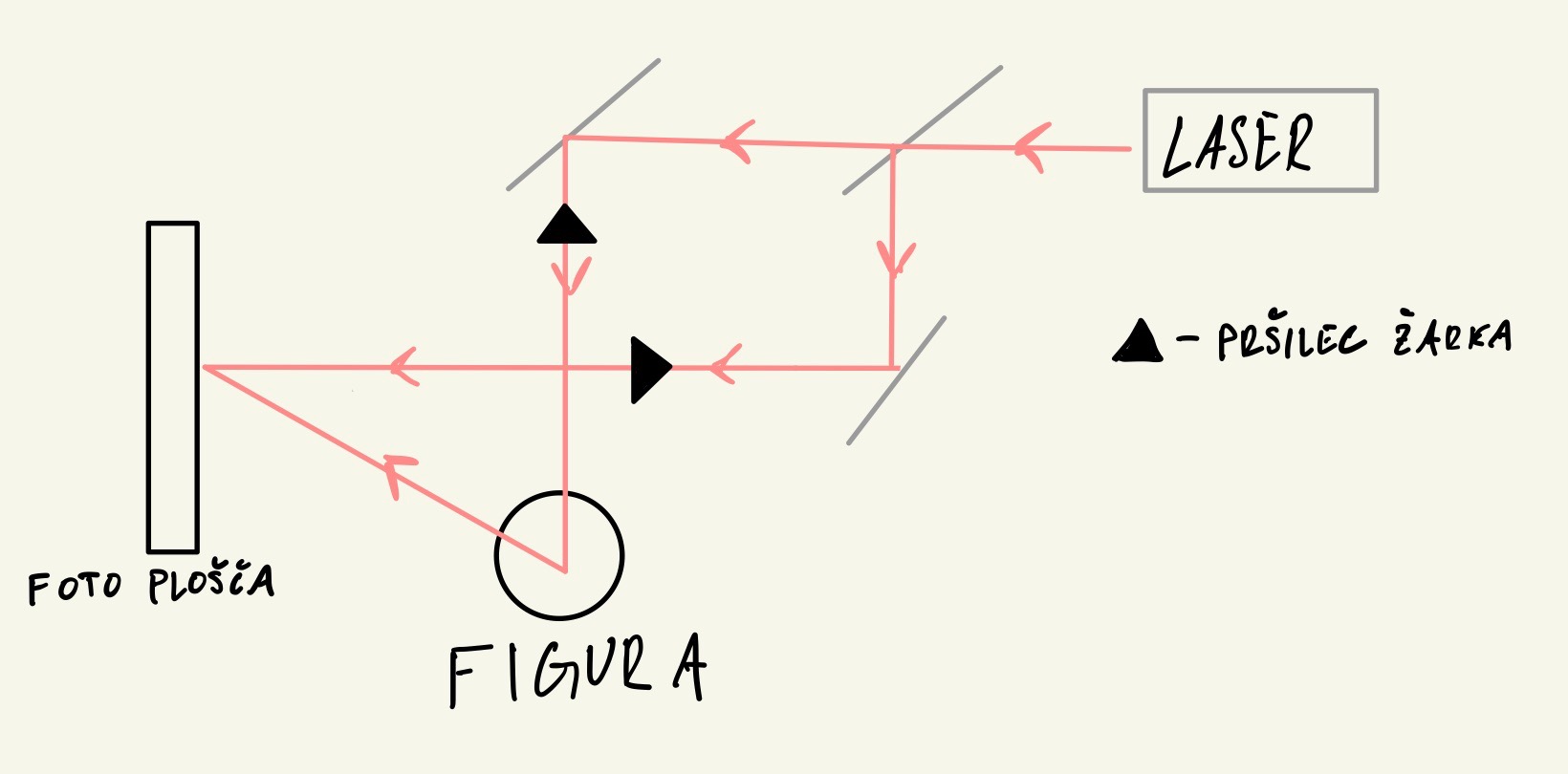
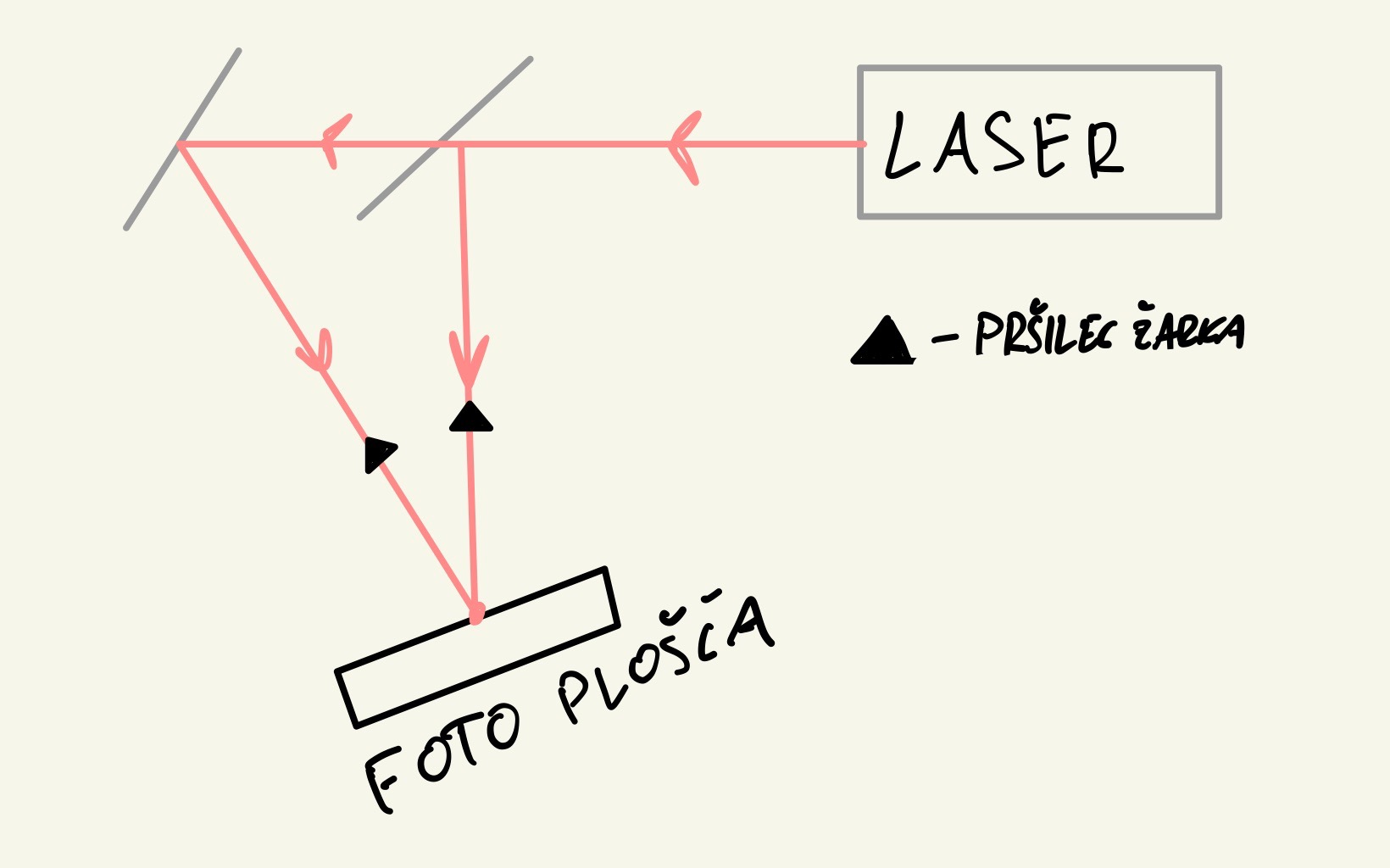
Svetlobno valovanje (električna poljska jakost) nosi podatek o globinski porazdelitvi posameznih točk na površini predmeta v fazi valovanja. Pri običajni fotografiji je ta podatek izgubljen, saj je počrnitev filma sorazmerna povprečni vrednosti kvadrata električne poljske jakosti, ki je neodvisna od fazne razlike. Pri holografskem zapisu ohranimo podatke o fazah tako, da s fotografsko ploščo registriramo interferenčno sliko, ki nastane pri interferenci med svetlobo, ki jo siplje predmet in svetlobo, ki na poti do fotografske plošče predmet obide.

Slika, ki tedaj nastane na fotografskem filmu na pogled s prostim očesom deluje precej nenavadna. Če figuro zamenjamo s točkastim izvorom, bi na fotografski film posneli vzorec, ki močno spominja na t.i. Fresnel zone plates. Posneta ploščica tedaj deluje kot neke vrste uklonska leča, ki ob prisotnosti koherentnega vira svetlobe z lečenjem poustvari tri žarke. To so: 1) originalni ravni val, 2) val, ki divergira stran od točkastega izvora - virtualna slika ter 3) val, ki konvergira in ga lahko opazimo npr. v cigaretnem dimu - realna slika. S kombiniranjem točkastih izvorov lahko tako "seštevamo" t.i. Fresnelove cone, da dobimo interferenčni vzorec za poljubno obliko izvora.

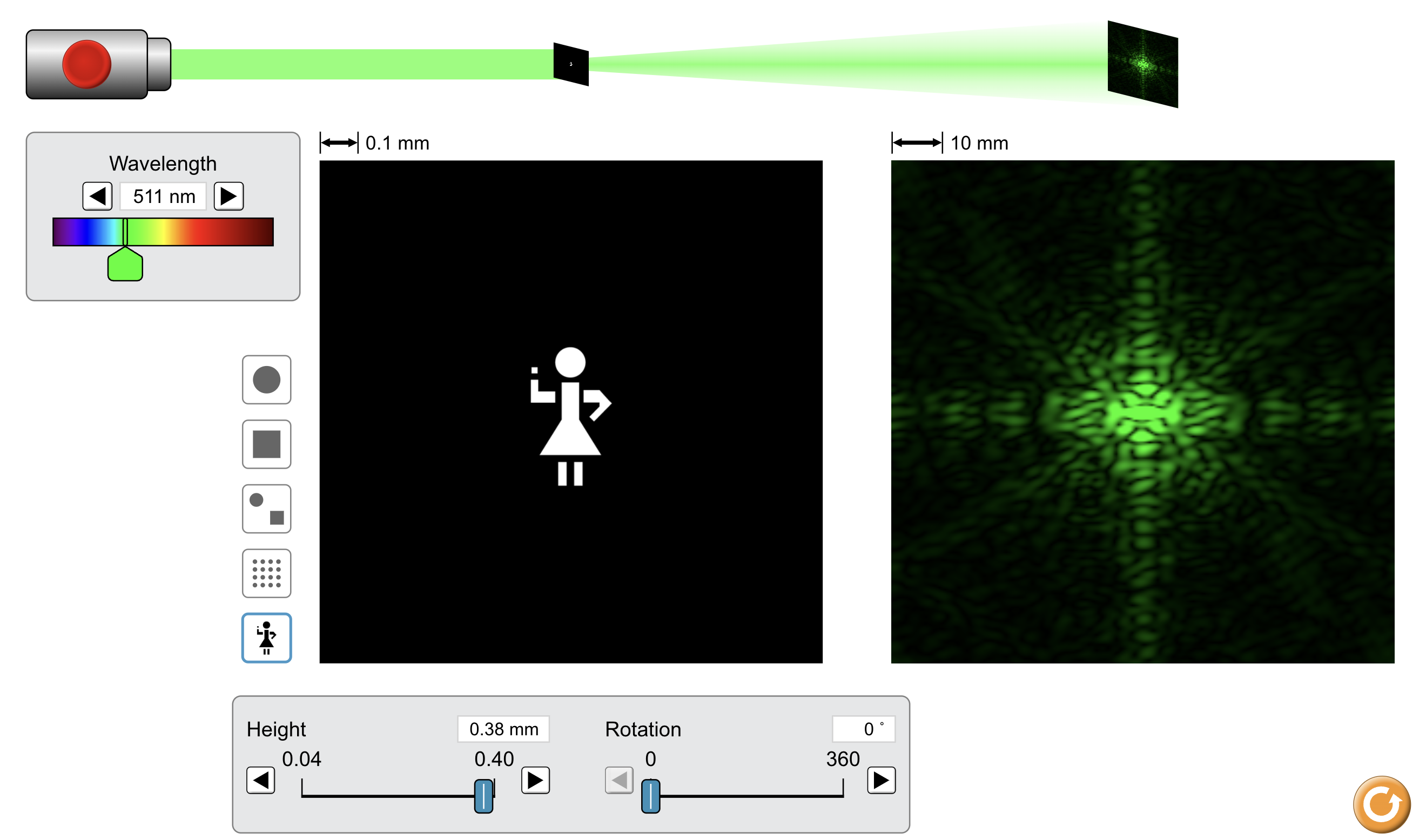
Slika 1: PhET Colorado animacija prikazuje uklonsko sliko pri izvoru v obliki figure. Vzorec nas do neke mere spominja na sliko, ki se s prostim očesom vidi na posneti ploščici našega holograma. Povezava do animacije

Naloga

1. Sestavi postavitev za snemanje holograma in ga posnemi!
2. Posnemi interferogram dveh ravnih valov!

Potrebščine

• laser
• polprepustno zrcalo
• 2x zrcalo
• 2x pršilec snopa
• zaslon
• kemikalije: razvijalec, voda, fiksir
• foto ploščica

1. Interferogram figure

Za snemanje interferograma figure postavimo inštrumente kot prikazuje shema (Slika 2). Laserski žarek pošljemo najprej skozi polprepustno zrcalo, ki ga razdeli na dva pravokotna snopa. Prvi snop s pomočjo zrcala pošljemo skozi pršilec in ga usmerimo na zaslon. Enako storimo za drugi žarek, le da tokrat ciljamo figuro. Poskrbimo, da je figura dobro osvetljena in da se žarka s figure ter referenčni snop iz laserja srečata na zaslonu, kjer interferirata. Na mesto zaslona postavimo foto steklce, izpostavimo laserju za 10s, namočimo v razvijalec, vodo, fiksir ter steklce spreremo pod tekočo vodo. V steklce posvetimo z laserjem in vanj pogledamo - opazimo hologramsko sliko figure.

Slika 2: Shema za interferogram figure

1.1 Matematična obravnava

Koordinatni sistem za opis valovanja postavimo tako, da njegova $(x,y)$ ravnina ujema s fotografsko ploščo. Svetlobno polje opišemo s poljem elektirčne poljske jakosti $E$. Privzamemo, zaradi lažje obravnave, da ima električna poljska jakost po odboju na predmetu isto smer kot pred odbojem. Privzamemo tudi, da ima $E$ ves čas samo eno komponento E, ki jo bomo obravnavali kot skalar.

V shemi obravnavamo referečni snop $E_r$ in predmetni snop $E_p$. Zapišemo:

$E_p(x,y) = E_{p0}(x,y) \exp{(-i \phi (x,y))} \exp{(i\omega t)}$

$E_r(x,y) = E_{r0}(x,y) \exp{(-i \psi (x,y))} \exp{(i\omega t)}$,

kjer sta $\psi$ in $\phi$ fazi valovanj. Ker sta valovanji koherentni, velja:

$I = (E_p + E_r)(E_p + E_r) = |E_p|^2 + |E_r|^2 + E_p E_r^* + E_p^* E_r $

Vidimo, da se v enačbi poleg intenzitete predmetnega in interferenčnega člena pojavita tudi mešana interferenčna člena, ki vsebujeta informacijo o relativnih fazah med predmetnim in referenčnim snopom. Počrnitev fotografskega filma je odvisna od ploskovne gostote energije, ki pade na emulzijo. Ta pa je enaka produktu gostote svetlobnega toka in časa osvetljevanja - označimo z $W_{ex}$.

Transmitivnost emulzije T v odvisnosti od ekspozicije je podana kot: $T \propto W_{ex}^\gamma \propto I^\gamma$. Parameter $\gamma$ je odvisen od lastnosti emulzije in načina razvijanja. Uporabimo prepostnost, ki je definirana kot:

$T_{ampl} = \sqrt{T}$

Upoštevamo, da je $E_p << E_r$ in dobimo:

$T_{ampl} = C |E_r|^\gamma \left( 1 + \frac{\gamma}{2|E_r|^2} (E_p E_r^* + E_p^* E_r) \right) = A + B E_p E_r^* + B E_p^*E_r $,

kjer sta A in B konstanti.

Po razvijanju hologram postavimo nazaj na zaslon, ga osvetlimo z referenčnim žarkom, predmet pa odstranimo. V tem primeru je električna poljska jakost na izstopni strani fotografske plošče $E_{holo}$ enaka produktu:

$E_{holo} = T_{ampl}E_r = AE_r + B|E_r|^{2}E_p + BE_r^2E_p^{*}$,

kjer prvi člen predstavlja prepuščeni referenčni snop, ki je delno oslabljen. DRugi člen opisuje divergenten snop žarkov, ki je tak, kot bi izhajal od predmeta. Pri prehodu skozi očesno lečo se zbere na mrežnici, kjer nam da realno sliko. Ker so valovne fronte, ki izhajajo iz holograma enake tistim, ki so izhajale od predmeta, zaznamo sliko, ki jo vidimo pri gledanjo golograma, kot tridimenzionalno.

Kaj pa pomeni tretji člen? Enačbo pomnožimo s kompleksno konjungiranim referenčnim valom - kar v realnosti pomeni snop, ki se širi v obratni smeri - dobimo:

$E_{holo} = T_{ampl}E_r^* = AE_r^* + BE_r^{*2}E_p + B|E_r|^2E_p^{*}$

Tretji člen je tedaj enak kompleksno konjungiranemu drugemu členu v prejšnji enačbi, torej predstavlja predmetni snop, ki se širi v nasprotni meri. Žarki v 3. členu so konvergentni in nam dajo realno sliko, ki bi jo lahko videli, če bilo v zraku dovolj delcev (npr. cigaretni dim).

Ko z referenčnim žarkom osvetljujemo hologram dobimo torej tri žarke; oslabljen referečni snop, divergentni snop, ki daje virtualno sliko predmeta in konvergentni snop, ki realno sliko predmeta. Pri dovolj veliko razdalji so snopi prostorsko ločeni. Hologramu rečemo transmisivni, prostorsko ločen hologram.

1.2 Rezultati

Uspešno smo posneli hologram figurice (Slika 3,4).

Slika 3: Fotografsko steklce osvetljeno z referenčnim žarkom

Slika 4: Efekt paralakse na stekelcu

2. Interferogram dveh ravnih valov

Z enakim postopkom posnamemo še interferogram dveh ravnih valov. Postavitev ekspremienta prikazuje Slika 5.

Slika 5: Shema za interferogram dveh ravnih valov

2.1 Matematična obravnava

Obravnavamo dva žarka oblike $e^{i(kr - \omega t)}$, od katerih prvi pada na fotografsko ploščo pod kotom $\alpha$ glede na normalo, drugi pa v smeri normale. Izberemo koordinatni sistem tako, da se valovna vektorja zapišeta kot $\vec{k_p} = (k \sin \alpha, 0, k \cos \alpha )$ in $\vec{k_r} = (0, 0, k)$. Privzamemo, da se fotografska plošča nahaja v ravnini $z = 0$. Potem je intenziteta interferenčnega vzorca na njej:

$I_{int} = C \; |1 + e^{i k \sin \alpha x}|^2 = C' (1+ \cos (k \sin \alpha x))$.

Hologram je kosinusna uklonska mrežica s periodo:

$d = \frac{2 \pi}{k \sin \alpha}$

Natančnejši izračun s Frauhoferjevim uklonskim integralom pokaže, da dobimo pri osvetlitvi kosinusne uklonske mrežice z ravnim valom poleg prepuščenega vala še dva uklonjena žarka prvega reda, ki sta razporejena simetrično levo in desno glede na prepuščeni val. Ustrezata 2. in 3. členu v enačbi za $E_{holo}$. Splošen tankoplastni hologram lahko razumemo kot superpozicijo kosinusnih uklonskih mrežic, ki nastanejo pri interferenci referenčnega žarka in žarkov, ki izvirajo iz posameznih točk objekta.

2.2 Rezultati

Uspešno smo posneli interferogram dveh ravnih valov (Slika 6,7). Kot med žarkoma razberemo iz slike, $\alpha \approx 17^\circ$. Hologrami višjih redov niso bili prisotni! (razen pričakovnega 1. reda)

Slika 6: Postavitev in kot med žarkoma

Slika 7: Ojačanje 0. reda ter ojačanje 1. reda na levi in desni pri osvetlitvi fotografskega steklca z referenčnim žarkom.

2.3 Ocena razdalje med maksimumi

Ocenimo po enačbi $d = \frac{\lambda * n}{\sin \alpha} = \frac{635 \textrm{nm}}{\sin 17^\circ \pm 1.5^\circ} = 2.2 \mu m \pm 0.3 \mu m$.

3. Zaključek

Pri vaji smo uspešno posneli interferogram figure ter interferogram valovanje dveh ravnih valov. Fotografska stekelca smo osvetlili z referenčnim žarkom in v njih oz. na zaslonu opazovali hologram. Ker na steklca snemamo interferenčni pojav, moramo paziti na resolucijo. Ocenili smo, da je razdalja med maksimumi pri valovni dolžini 635 nm enaka $ d = 2.2 \mu m \pm 0.3 \mu m$, kar je dovolj veliko, da nas tresenje mize ipd. ne moti pri snemanju holograma. Prav tako je ta meja blizu resolucije foto emulzije (cca 1000 črt na 1mm).