Uvod¶
Feroelektrične smektične $C^*$ tvorijo molekule, ki imajo velik električni dipolni moment prečno na vzdolžno os molekul, zato se v teh snoveh pojavi električna polarizacija, ki leži v ravnini plasti in je pravokotna na direktor. Približno je sorazmerna s kotom nagiba. Zaradi vijačne strukture je makroskopska električna polarizacija vzorca enaka. Polarizacijo plasti lahko uredimo v isto smer bodisi z zunanjim električnim poljem bodisi tako, da vzorec ogradimo s ploščicama, ki predpisujeta orientacijo molekul. Če postavimo tanek površinsko stabiliziran feroelektrični kristal v zunanje električno polje, se spremeni optična os vzorca. Linearnemu odzivu lomnega količnika snovi na zunanje električno polje pravimo elektrooptični pojav.
Odvisnost spremembe polarizacije od frekvence lahko opišemo z Debyjevim relaksacijskim modelom:
$ \delta P = \delta P_0 \frac{1}{1 + i \omega \tau} $
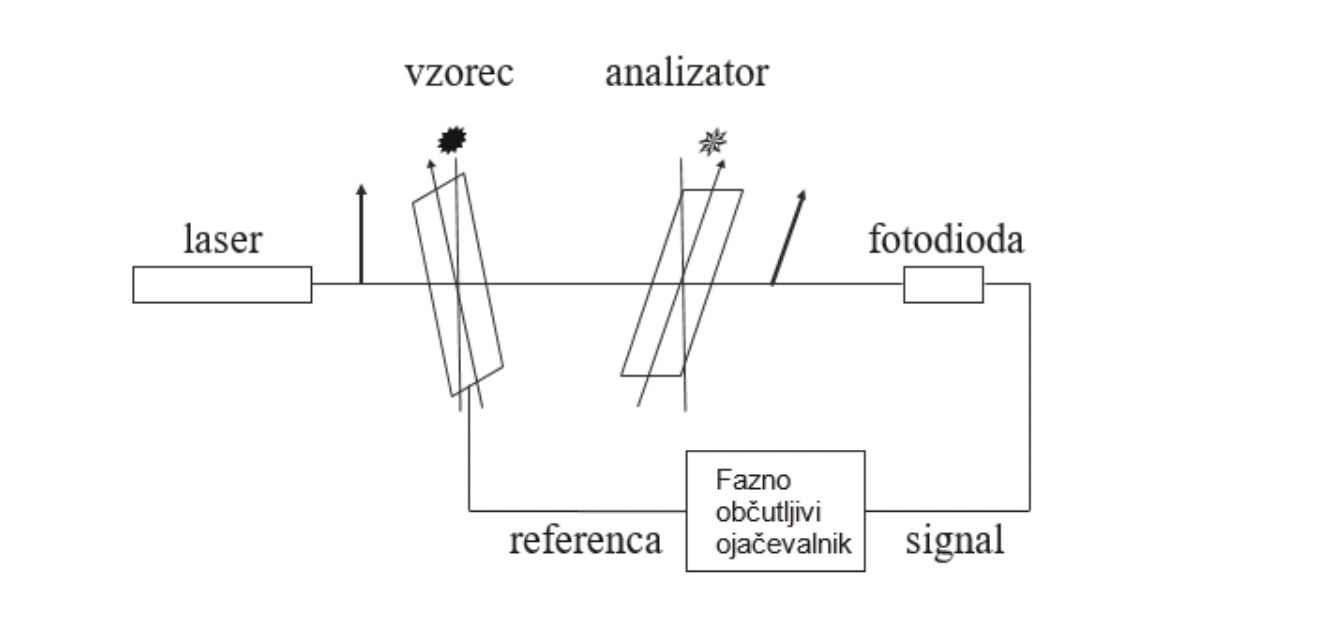
Spremembo smeri optične osi vzorca lahko zaznamo tako, da opazujemo , kako se spremeni polarizacija svetlobe pri prehodu skozi vzorec. Prepuščeno moč merimo s fotodiodo, s fazno občutljivim ojačevalnikom pa spremljamo napetost na delovnem uporu.
V tekočem kristalu je zasuk optične osi $ \psi $ zaradi viskoznosti snovi zakasnjen glede na zunanje električno polje. Del, ki je v fazi, dobimo kot realni del Debyjevega relaksacijskga modela, del, ki je premaknjen za $ \pi / 2 $ pa kot imaginarni del te iste enačbe:
$ \psi_R = \frac{ \psi_0 }{1 + (\omega \tau)^2} $
$ \psi_{Im} = \frac{ \psi_0 \omega \tau }{1 + (\omega \tau)^2} $
Iz izmerjenih $\psi_R$ in $\psi_{Im}$ lahko dobimo relaksacijski čas $\tau$ s prilagajanjem gornjih izrazov meritvam. Imamo pa še drugo zanimivo možnost. Če narišemo razmerje med $\psi_R$ in $\psi_{Im}$ ter linearno aproksimiramo, dobimo premico, iz katere lahko izrazimo $\tau$.

Slika 1: Struktura smektične $C^*$ faze: molekule ležijo v plasteh, povprečna smer molekul opiše vijačnico v smeri normale plasti